Find Constant Rate Of Change

CONSTANT RATE OF Modify

A rate of change is a rate that describes how one quantity changes in relation to another quantity.

Constant charge per unit is also called every bit compatible rate which involves something travelling at fixed and steady stride or else moving at some average speed.

For example, A car travels 3 hours. It travels 30 miles in the first hour, 45 miles in the second hour and 75 miles in the 3rd hour.

Speed in the outset hr = xxx miles/hour

Speed in the 2d hr = 45 miles/hour

Speed in the third hour = 75 miles/hour

Nosotros accept three different speeds in the three hour journey.

If we want to notice the constant rate for the whole journey of three hours, we have to find the ratio between the total distance covered and total time taken.

That is, constant rate = (30 + 45 + 75)/three

= 150/3

= 50 miles/hour

Based on the above example, the formula is to discover the abiding speed is given below.

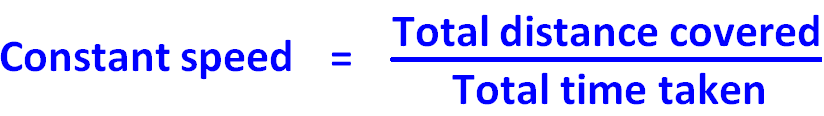
If a person travels from A to B at some speed, say 10 miles per hour. He comes back from B to A at dissimilar speed, say y miles per hour. Both the means, he covers the same distance, but at different speeds.

Then, the formula is to find the constant speed for the whole journey is given below.

Solved Examples

Instance ane :

David drove for 3 hours at a rate of l miles per hour, for 2 hours at 60 miles per hour and for 4 hours at a rate of lxx miles per hr. What was his constant-speed for the whole journey ?

Solution :

Step one :

Formula for constant speed :

= Full distance/Total fourth dimension taken

Formula for distance :

= Rate x Fourth dimension

Step 2 :

Distance covered in the get-go 3 hours :

= 50 x three

= 150 miles

Distance covered in the next 2 hours :

= 60 ten 2

= 120 miles

Distance covered in the concluding 4 hours

= 70 x v

= 350 miles

Footstep 3 :

Then,

full distance = 150 + 120 + 350 = 620 miles

full fourth dimension = 3 + 2 + five = ten hours

Stride 4 :

So, constant speed is

= Full altitude/Total time taken

= 620/10

= 62 miles per hour

Instance two :

A person travels from New York to Washington at the rate of 45 miles per hr and comes backs to the New York at the rate of 55 miles per hour. What is his abiding-speed for the whole journey ?

Solution :

Step 1 :

Hither, both the ways, he covers the same distance.

Then, formula for constant speed = 2xy/(x + y)

Step ii :

10 ----> Charge per unit at which he travels from New York to Washington.

x = 45

y ----> Rate at which he travels from New York to Washington

y = 55

Stride iii :

So, abiding speed is

= 2(45)(55)/(45 + 55)

= 4950/100

= 49.five miles per hour

Example 3 :

A man takes 10 hours to become to a identify and come back by walking both the ways. He could accept gained 2 hours by riding both the ways. The distance covered in the whole journey is 18 miles. Find the constant speed for the whole journey if he goes by walking and comes back by riding.

Solution :

Step 1 :

Walking + Walking = ten hours -----> walking = 5 hours

Riding + Riding = 8 hours (Because 2 hours gained)

So, Riding = 4 hours

Walking + Riding -----> ( 5 + four ) = ix hours

Footstep 2 :

Full fourth dimension taken = 9 hours

Total distance covered = 18 miles

Stride 3 :

So, constant speed is

= Total distance/Total time taken

= 18/nine

= 2 miles per hour

Example four :

David travels from the place A to identify B at a certain speed. When he comes back from place B to place A, he increases his speed 2 times. If the constant-speed for the whole journey is fourscore miles per hour, find his speed when he travels from the identify A to B.

Solution :

Step ane :

Allow 'a' be the speed from place A to B.

Then, speed from identify B to A = 2a

Step 2 :

Here, both the ways, he covers the same distance.

And so, formula for abiding speed = 2xy/(x + y)

Step three :

x ----> Speed from place A to B

x = a

y ----> Speed from place B to A

y = 2a

Stride 4 :

Given : Constant speed = 80 miles/hour

2(a)(2a)/(a + 2a) = 80

4a²/3a = 80

4a/3 = fourscore

a = sixty

Speed from identify A to B is 60 miles per hour.

Example 5 :

Kemka is preparing 20 cups of apple juice in the first 4 minutes and 60 cups in the adjacent 12 minutes. How many cups does she ready per minute ?

Solution :

Step 1 :

Total no. of cups of apple juice prepared is

= 20 + sixty

= 80 cups

Stride two :

Total time taken is

= 4 + 12

= 16 minutes

Stride 3 :

Number of cups of apple juice prepared per minute is

= Total number of cups/Total time taken

= eighty/16

= 5

Kemka prepares five cups of apple juice per minutes.

Kindly mail your feedback tov4formath@gmail.com

We ever appreciate your feedback.